正版软件_购买stata软件以及培训班

科学软件网提供的软件上千款，涉及所有学科领域，您所需的软件，我们都能提供。科学软件网提供的软件涵盖领域包括经管，仿真，地球地理，生物化学，工程科学，排版及网络管理等。同时，还提供培训、课程（包含34款软件，66门课程）、实验室解决方案和项目咨询等服务。
You can also use the styles shipped with Stata or styles created by your colleagues.
Let's create a table using the collection system. We grab the NHANES II data (McDowell et al. 1981) that are used in many examples in the manuals.

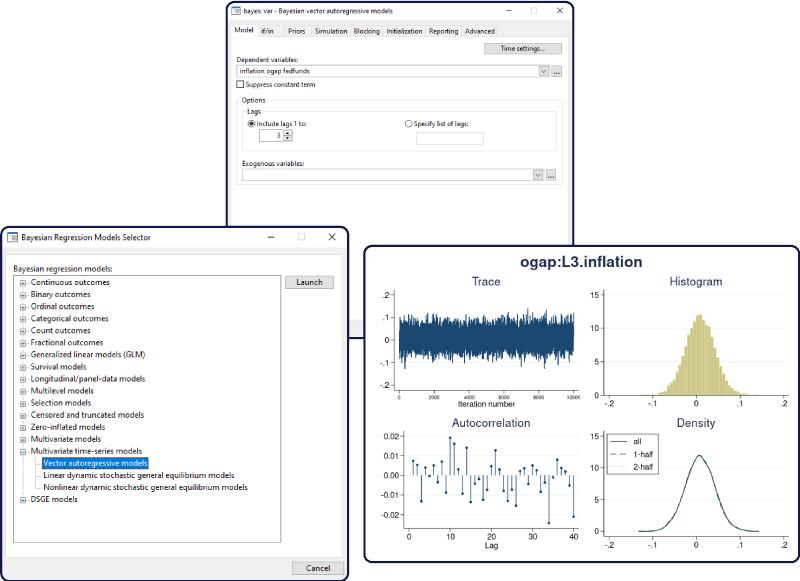
What is Bayesian analysis?
Bayesian analysis is a statistical analysis that answers research questions about unknown parameters
of statistical models by using probability statements. Bayesian analysis rests on the assumption that
all model parameters are random quantities and thus are subjects to prior knowledge. This assumption
is in sharp contrast with the more traditional, also called frequentist, statistical inference where all
parameters are considered unknown but fixed quantities. Bayesian analysis follows a simple rule
of probability, the Bayes rule, which provides a formalism for combining prior information with
evidence from the data at hand. The Bayes rule is used to form the so called posterior distribution of
model parameters. The posterior distribution results from updating the prior knowledge about model
parameters with evidence from the observed data. Bayesian analysis uses the posterior distribution to
form various summaries for the model parameters including point estimates such as posterior means,
medians, percentiles, and interval estimates such as credible intervals. Moreover, all statistical tests
about model parameters can be expressed as probability statements based on the estimated posterior
distribution.

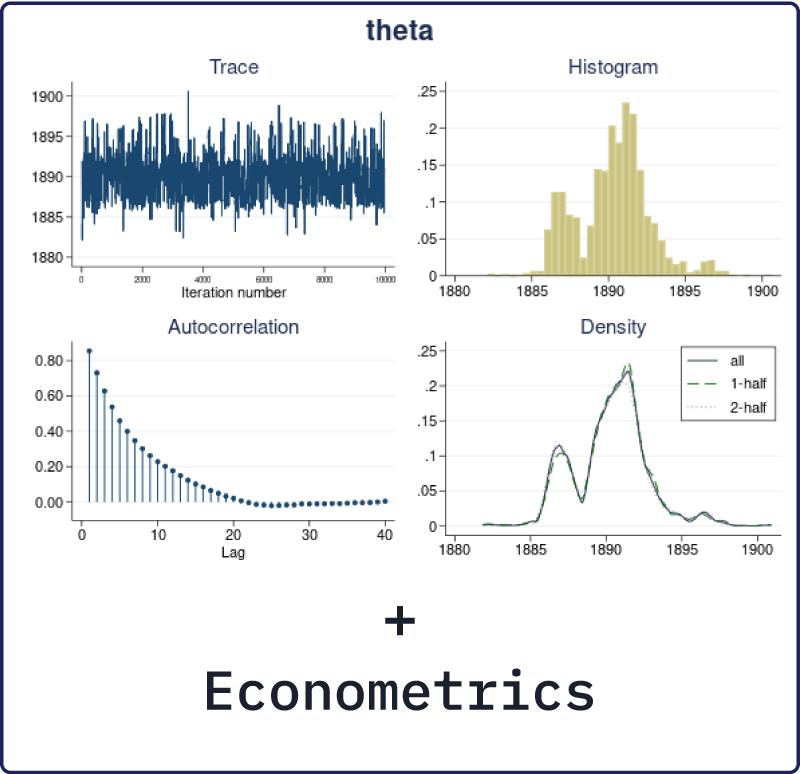
In Bayesian analysis, we can use previous information, either belief or experimental evidence, in
a data model to acquire more balanced results for a particular problem. For example, incorporating
prior information can mitigate the effect of a small sample size. Importantly, the use of the prior
evidence is achieved in a theoretically sound and principled way.
By using the knowledge of the entire posterior distribution of model parameters, Bayesian inference
is far more comprehensive and flexible than the traditional inference.
Bayesian inference is exact, in the sense that estimation and prediction are based on the posterior
distribution. The latter is either known analytically or can be estimated numerically with an arbitrary
precision. In contrast, many frequentist estimation procedures such as maximum likelihood rely on
the assumption of asymptotic normality for inference.

主讲嘉宾
王存同，人口学博士、教授。博士毕业于北京大学（与University of Michigan合作培养)，博士后研究员就职于美国伊利诺伊大学（University of Illinois at Urbana-Champaign）。现为财经大学社会发展学院教授，主要从事社会统计及计量经济分析、人口社会学、人口经济学等领域的研究与教学，其定量研究与教学在国内外学术界享有较高的盛誉。
科学软件网不定期举办各类公益培训和讲座，让您有更多机会免费学习和熟悉软件。
http://www.kxrjsoft.com.cn